Wat je leert van 1.030 turfjes en 27.740 Skittles

Beste,

Afgelopen maandag hield ik mijn tweede theatercollege, ditmaal in TivoliVredenburg. Bedankt, iedereen die erbij was, voor de mooie avond! Voor de rest: er zijn opnames gemaakt, die binnenkort op De Correspondent zullen verschijnen.

Mijn boodschap van de avond zal je niet verbazen: we moeten kritisch zijn op cijfers. Maar té kritisch is ook weer niet goed. Zoals collega Joris Luyendijk zegt: ‘Iemand die besluit niks meer te geloven is net zo naïef als iemand die alles gelooft.’

Ik gebruikte het begin van het college daarom ook om te onderstrepen waarom cijfers belangrijk zijn. De eerste reden: door cijfers kunnen we op grote schaal samenwerken.

Lang, lang geleden leefden we in kleine gemeenschappen. De belangrijke informatie kon je opslaan in je hoofd: waar de giftige bessen groeiden, wie je kon vertrouwen, welke plekken je moest vermijden.

Maar naarmate we in grotere gemeenschappen zijn gaan leven – steden, landen, unies – werden de (economische) relaties steeds ingewikkelder. Je kreeg nog geld van de ene, had een schuld bij de ander, moest belasting betalen aan een derde.

We konden niet meer alles onthouden. Daar bedachten we een oplossing voor: het schrift. En veel van wat werd opgeschreven, bevatte cijfers. Neem een kleitablet Bekijk het kleitablet. uit het vierde millennium voor Christus waarop staat ‘29.086 maten gerst 37 maanden Kushim’.

Het is een beroemd kleitablet geworden, want Kushim is misschien wel de eerste persoon van wie we de naam kennen. ‘Het is veelzeggend’, schrijft historicus Yuval Noah Harari in zijn boek Sapiens, ‘dat de eerste vastgelegde naam in de geschiedenis toebehoort aan een boekhouder en niet aan een profeet, een dichter of een grote veroveraar.’

John Snow

Maar er is nog een reden dat cijfers belangrijk zijn: ze helpen om patronen te ontdekken. Het verhaal van John Snow is daar een mooie illustratie van. (Mocht je een pavlovreactie krijgen: nee, ik ga het niet hebben over Game of Thrones.)

John Snow is ‘de vader van de epidemiologie’ en leefde in de negentiende eeuw. Cholera, een infectieziekte die ernstige diarree kan veroorzaken en de patiënt soms binnen een paar uur doet overlijden, was in die tijd een groot probleem.

Artsen vermoedden dat de ziekte door ‘miasmata’ kwam, deeltjes in de lucht. Gore lucht, zeg maar. Maar Snow geloofde niet in deze miasmatheorie. Hij was ervan overtuigd dat de ziekte zich via water verspreidde. Het was alleen wachten op de juiste situatie om zijn idee te bewijzen.

Die situatie kwam in 1854, toen in een Londense buurt cholera uitbrak. Snow toog met een collega naar de straten rond Broad Street om data te verzamelen. Later noteerde hij zijn bevindingen op een kaart (hoe groter een staafje, des te meer choleragevallen Snow op die plek had gevonden).

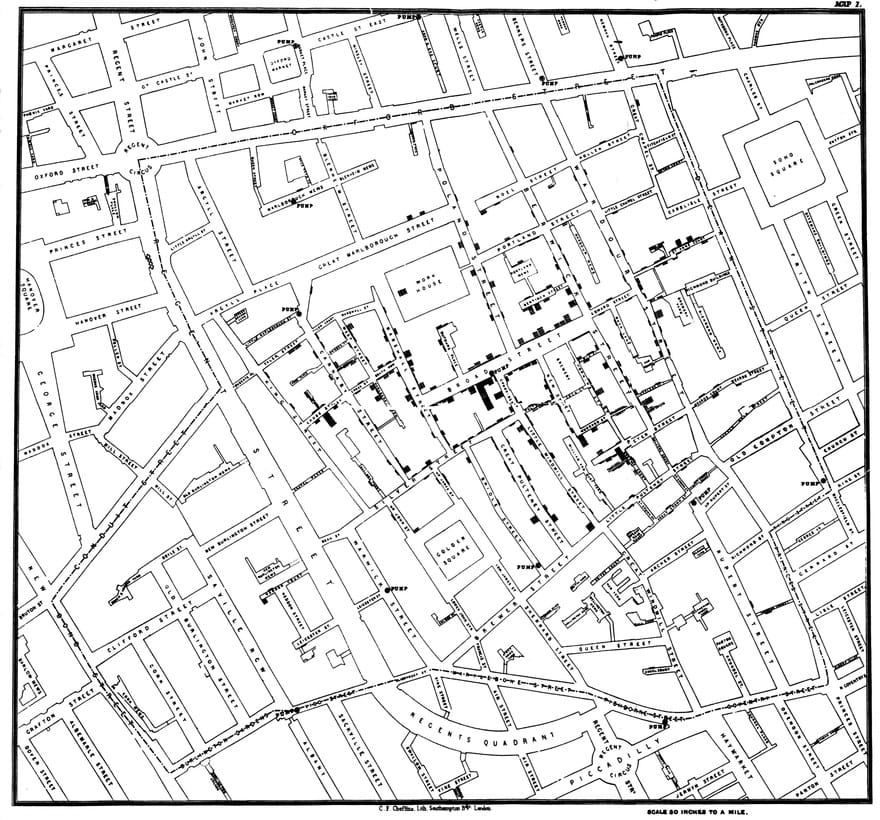
Precies in het midden van de uitbraak zie je, als je heel goed kijkt, een waterpomp. Dat was de boosdoener, concludeerde Snow. Maar de mensen die dezelfde waterpomp gebruikten, ademden ook dezelfde lucht in. Het konden dus alsnog de miasmata zijn.

Daarom kwam Snow met twee extra bewijsstukken. Eén, een buurtbewoner had het water – dat bekendstond om zijn lekkere smaak – meegenomen naar een tante en een nicht. Ook zij waren ziek geworden.

Twee, de brouwerij om de hoek van de pomp had zijn eigen bron én werknemers mochten ongelimiteerd bier drinken. Daar was juist weer bijna niemand ziek geworden.

Zo had Snow bewezen dat de cholera-uitbraak door het water kwam. Later bleek dat een vieze luier in de waterpomp op Broad Street terecht was gekomen. Het zou nog lang duren, maar uiteindelijk nam de medische gemeenschap afscheid van de miasmatheorie.

De macht van de enen

Een heel ander voorbeeld van patroonherkenning is de wet van Benford. Men neme een berg getallen, bijvoorbeeld van een beurspagina uit Het Financieele Dagblad.

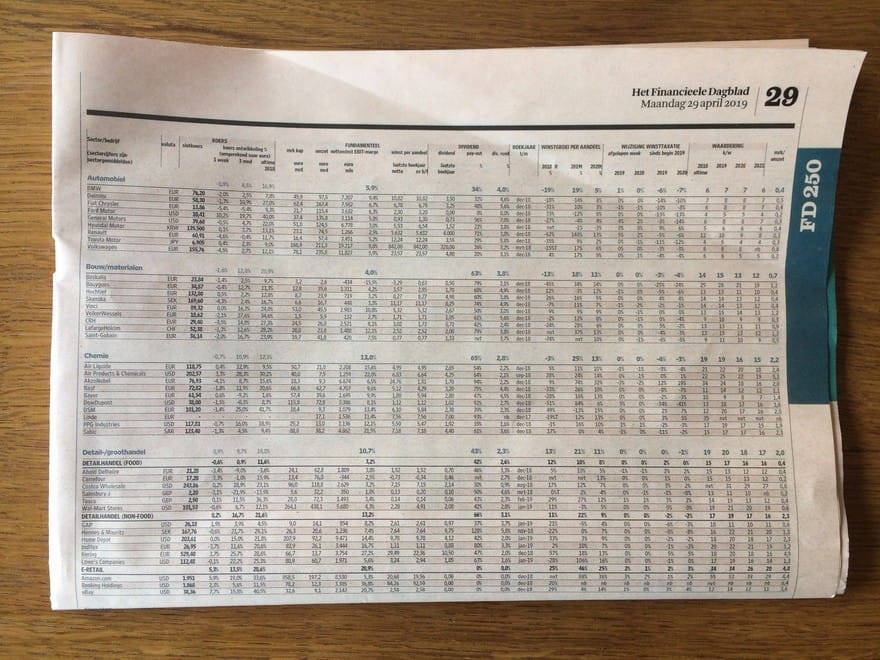
Noteer nu van alle getallen telkens het eerste cijfer. Van 118,75 pak je de 1. Van 202,57 de 2. Van 76,93 de 7. Et cetera.

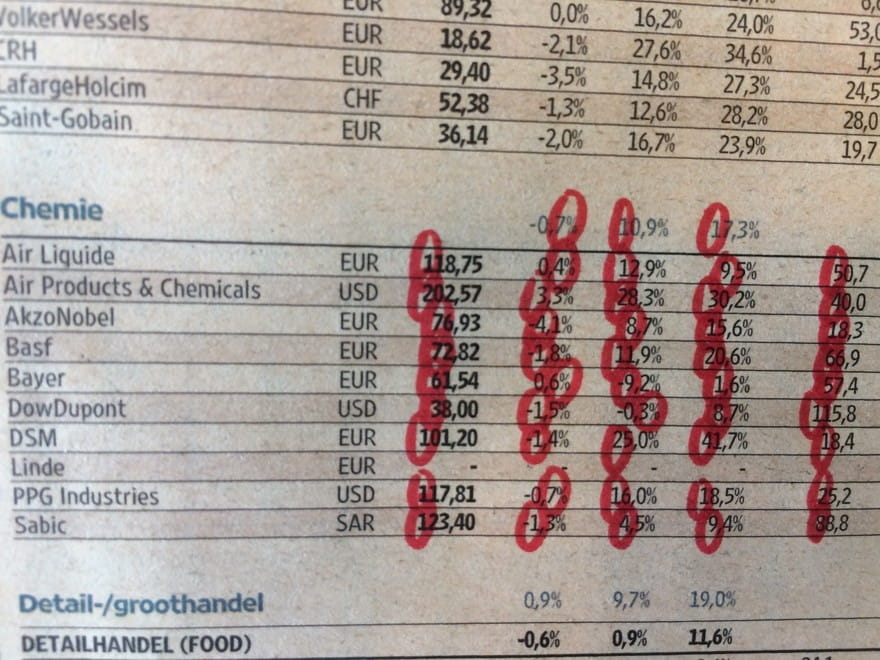
Tel nu voor elk van de negen begincijfers (1, 2, 3, 4, 5, 6, 7, 8, 9) hoe vaak ze voorkomen. Hoe vaak, denk je, zal de 1 voorkomen?

Je intuïtie – de mijne in ieder geval wel – zegt waarschijnlijk 1 op de 9 keer. Het lijkt logisch dat zo’n 11 procent van de begincijfers een 1 is. En dat de andere cijfers ieder ook 11 procent van de keren voorkomen.

Maar als je gaat turven zie je iets anders. Ik turfde...

..

...en turfde...

...en turfde...

...en na 1.030 turfjes zag ik: de 1 komt veel vaker voor dan 11 procent.

De fysicus Frank Benford berekende hoe vaak je kunt verwachten dat elk begincijfer voorkomt in een grote verzameling getallen (‘de wet van Benford’). De cijfers uit het FD volgen Benfords percentages, met hooguit een paar procentpunten verschil.

Dus?

Ik kan me voorstellen dat je niet direct het nut inziet van mijn eindeloze geturf. Maar de wet van Benford kan erg nuttig zijn. Bij het opsporen van fraude wordt regelmatig gebruikgemaakt van de wetmatigheid.

Neem de economische cijfers van Griekenland, die jarenlang werden opgepoetst. Zonder die manipulatie zou Griekenland misschien wel nooit tot de Eurozone zijn toegelaten.

Kijk je naar data van 27 EU-landen, dan zie je dat de begincijfers netjes bij de wet van Benford passen. Maar kijk je naar Griekenland, dan zie je dat het land sterk uit de pas loopt.

Natuurlijk is het afwijken van de wet van Benford geen garantie dat er sprake is van fraude. Andersom geldt hetzelfde: al zien de data er goed uit, er kan toch iets niet in de haak zijn. Bernie Madoff – een van de grootste fraudeurs in de geschiedenis – had cijfers die Benfordfähig waren.

Maar het is wel een alarmbel voor mogelijke problemen. En zo zie je weer: cijfers kunnen helpen om patronen te ontdekken, in dit geval frauduleus gedrag.

Meer lezen over de wet van Benford? Collega Thalia Verkade schreef er een paar jaar geleden een stuk Lees het stuk van Thalia. over.

#NerdAlert

Dan een actie waarbij mijn geturf in het niet valt. Een wiskundige berekende Lees de blogpost over de Skittles. hoeveel zakjes Skittles hij moest openmaken tot hij twee identieke (van elk van de vijf kleuren hetzelfde aantal snoepjes) zou vinden. Hij kwam op vierhonderd tot vijfhonderd.

Het is een opdracht die je zomaar bij een vak wiskunde zou kunnen krijgen. Maar wat de wiskundige vervolgens deed was onconventioneel: hij besloot te testen of zijn berekening klopte.

82 dagen, 468 zakjes en 27.740 Skittles later was het zover: hij had twee dezelfde gevonden. En jawel, zijn berekening van vierhonderd tot vijfhonderd bleek accuraat.

Tot slot...

...was er veel kritiek op het rekenmodel voor subsidies op elektrische auto’s. Maar, schrijft collega Jesse Frederik, Lees het stuk van Jesse. de schuldige was niet de man achter het rekenmodel. Het was de Tweede Kamer.

Met dank aan Leon de Korte, die me wees op het verhaal van John Snow. En aan Hans Pieter van Stein Callenfels voor de Skittles-tip. Het verhaal over Kushim beschreef ik eerder in Het bestverkochte boek ooit (met deze titel). Lees meer over mijn boek.

Deze nieuwsbrief liever in je inbox? Als correspondent Ontcijferen onderzoek ik de getallenwereld. In mijn nieuwsbrief houd ik je op de hoogte van wat ik schrijf, zie, hoor en lees. Een vast onderdeel: #NerdAlert, voor de getallenliefhebbers. Schrijf je in voor mijn nieuwsbrief