Wat het cijfer 1 allemaal over ons prijsgeeft

In willekeurig lijkende cijferreeksen, zoals de lengtes van rivieren of banktransacties, blijkt een onverwachte logica te zitten. Getallen die met een één beginnen, komen veel vaker voor. Met die kennis kun je fraude opsporen en het gedrag van aardbevingen doorgronden. Intussen begrijpt niemand hoe dat kan.
In 1881 bladerde de astronoom Simon Newcomb door een beduimeld naslagwerkje met logaritmische tabellen. Die liepen op van cijfers die begonnen met een één tot cijfers die begonnen met een negen.
Opvallend, dacht Newcomb. De eerste bladzijden van het boekje waren veel smoezeliger dan de rest. Waarom zochten zijn collega’s vooral getallen op die met enen en tweeën begonnen? En waarom bijna geen getallen die met een acht of een negen begonnen?
Na enig nadenken concludeerde Newcomb: omdat getallen die met een één beginnen veel vaker voorkomen dan getallen die beginnen met een twee, die op hun beurt vaker voorkomen dan getallen die beginnen met een drie, en ga zo maar door.
De astronoom was daar niet heel verbaasd over. Reden dat hij er niet verder indook en geen wiskundige wet naar zich vernoemd kreeg.
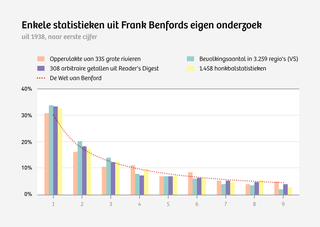
Die eer ging ruim een halve eeuw later naar ingenieur Frank Benford van het Amerikaanse elektriciteitsbedrijf General Electric. Hij toonde hetzelfde patroon aan in ruim twintigduizend cijfercombinaties. Denk aan de lengtes van rivieren, bevolkingsaantallen, willekeurige cijfers uit krantenartikelen, het gewicht van atomen, honkbalstatistieken en sterftecijfers.
Of het nu over kilometers, mensenlevens of grammen ging, in elk van deze verzamelingen trof Benford min of meer dezelfde getallendistributie aan, waarbij het getal 1 in grofweg dertig procent van de gevallen het begincijfer was, het getal 2 bijna de helft minder vaak begin cijfer was, en elk opvolgend getal nog minder vaak. Benford koppelde er als eerste een wiskundige formule aan. En zo ging het patroon de wiskundige geschiedenis in als de wet van Benford, ofwel: de wet van het Eerste Cijfer.
Patronen in mijn pin- en jullie leesgedrag
Waarom zouden getallen die met een negen beginnen niet even vaak voorkomen als getallen die met een één beginnen? Ik las voor het eerst over de wet van Benford in De Dronkemanswandeling van Leonard Mlodinow. Ondertitel: Hoe toeval ons leven bepaalt.
De wet van Benford lijkt echter juist aan te tonen dat regelmaat ons leven bepaalt, zonder dat we dat doorhebben. Ik kon het aanvankelijk nauwelijks geloven. Als het waar was, zou mijn eigen gedrag dan ook aan deze wetmatigheid voldoen?
Ja. Zie hieronder de frequentie van eerste cijfers in de afgelopen vijftien maanden aan bij- en afschrijvingen van mijn bankrekening, een kleine 750 transacties.
In mijn uitgaven- en inkomstenpatroon gedraag ik mij ongeveer zoals Frank Benford voorspelde vier decennia voordat ik überhaupt geboren was:
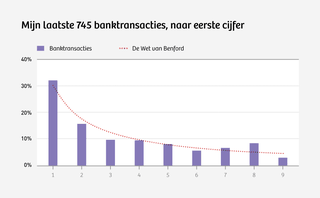
Zie hier de bron bij de grafiek.
En ook jullie, gewaardeerde leden van De Correspondent, gedragen je voorspelbaar. Hieronder zie je, steeds naar eerste cijfer, hoeveel seconden leden besteden aan het lezen van een artikel. Hoeveel artikelen jullie gezamenlijk lezen. En hoe vaak jullie artikelen delen. Al deze cijfers betreffen de leden van De Correspondent – niet de lezers van buiten.
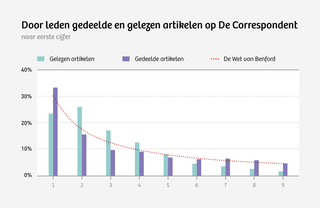
Zie hier de bron bij de grafiek.
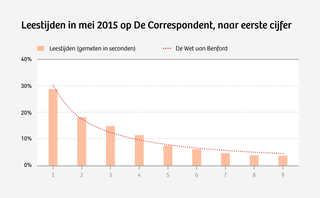
Zie hier de bron bij de grafiek.
Hetzelfde patroon is inmiddels gevonden
- in het aantal huisbezoeken dat Jehovah’s Getuigen afleggen per gemeente;
- in de belastingopgaven van Sicilianen;
- in biologische fenomenen als de verspreiding van infectieziekten;
- in de afstanden tot de ons bekende sterren;
- bij allerlei wiskundige reeksen, zoals de machten van 2 en 3 en de Fibonaccigetallen (de cijferreeks die je krijgt als je elk volgend getal optelt bij het vorige).
En dit zijn maar een paar voorbeelden.
De wet gaat ook op voor tweede en volgende cijfers in getallenreeksen, maar is weer niet zo alomtegenwoordig als licht of zwaartekracht. Sowieso vind je het patroon niet in begrensde verzamelingen, zoals geboortedata, postcodes of het aantal vakjes op de roulettetafel.
De herverkiezing van president Ahmadinejad
Ook verkiezingsuitslagen hoeven zich niet naar de wet te gedragen.
Bij de Iraanse verkiezingen van 2009 keek een onderzoeker naar anomalieën die zouden wijzen op fraude door onder meer het kamp van president Mahmoud Ahmadinejad. Maar een breder onderzoek over de toepasbaarheid van de wet van Benford op verkiezingen maakte gehakt van die gedachte. In Amerika veroorzaken kiesdistricten voorspelbare, maar niet Benfordiaanse patronen.
Bij verkiezingen spelen allerlei niet-willekeurige factoren een rol, zoals de neiging van mensen op grote partijen te stemmen en partijen die dreigen de kiesdrempel niet te halen, te negeren. Wat deze onderzoekers betreft was er dan ook geen logische reden om aan te nemen dat verkiezingsuitslagen zich zouden voegen naar de wet.
Dit toont meteen een moeilijkheid aan van de wet: we kunnen niet voorspellen wanneer die wel en niet geldt. Want wanneer is iets een niet-willekeurige factor?
Intussen worden er wel meer en meer toepassingen mee ontwikkeld.

Wat kun je hiermee?
Met de programmeertaal R kun je inmiddels met een paar drukken op de knop een boekhouding langs de wet van Benford leggen, iets wat accountants tegenwoordig ook doen.
De Nederlandse Belastingdienst zegt desgevraagd te overwegen de wet te gaan gebruiken om onregelmatigheden op te sporen als deze iets toevoegt aan de huidige set instrumenten.
Mensen blijken niet erg goed in het nabootsen van het toeval
En fraudeopsporing? Mensen blijken niet erg goed in het nabootsen van het toeval. Laat studenten verzinnen hoe een reeks van tweehonderd kop-of-muntworpen eruitziet, dan zullen ze nooit zes keer kop of zes keer munt achter elkaar laten vallen: dat lijkt te onwaarschijnlijk. In werkelijkheid is de kans dat er zes keer achter elkaar kop of munt valt in een serie van tweehonderd worpen bijna honderd procent.
Op dezelfde manier kunnen de meeste mensen niet overtuigend hun boekhouding vervalsen. Beroemd is het verhaal van een Amerikaanse ondernemer die zelf 91 miljoen dollar van investeerders uitgaf aan huizen, auto’s en ander speelgoed en dat probeerde te verhullen. Een forensisch accountant met de magische naam Darrell D. Dorrell liep de boekhouding van de man door en kreeg hem uiteindelijk veroordeeld tot twintig jaar cel. Details ontbreken, maar het verhaal gaat dat de wet van Benford de accountant op het goede spoor bracht.
Wanneer een fraudeur eenmaal op de hoogte is van de wet van Benford, wordt het natuurlijk een ander verhaal. De Canadese ondernemer Paul Kedrosky, die de inkomsten van oplichter Bernard Madoff analyseerde, concludeerde dat diens boekhouding zich zo perfect hield aan de wet van Benford, dat dat feit op zichzelf verdenking had moeten oproepen.

Steeds meer toepassingen
Door de brede geldigheid van de wet van Benford en de exponentieel groeiende berg digitale gegevens over ongeveer alles, worden er steeds meer toepassingen ontdekt voor de wet van Benford.
Dit voorjaar bleek dat je met de wet bots kunt opsporen – stukjes software die zich proberen te gedragen als mensen. Jennifer Golbeck analyseerde een kleine tachtigduizend Twitteraccounts met minstens honderd volgers en keek vervolgens naar het aantal volgers dat die accounts weer hadden. Dat leverde bijna altijd een keurig Benfordiaans grafiekje op.
De meeste accounts die grote afwijkingen lieten zien, bleken te behoren tot een netwerk van Russische Twitterbots die geautomatiseerd literaire citaten op Twitter slingerden. Wie er achter dit netwerk zit en waar deze activiteit op slaat, wordt nog onderzocht.
Omdat de wet evengoed opgaat voor menselijke als natuurkundige processen, kunnen bijvoorbeeld ook geologen er gebruik van maken. Zo blijken bij grote aardbevingen de aardschokken (de diepte waarop de trillingen plaatsvinden) zich te voegen naar de wet van Benford. Nu we dat weten, kan de wet wellicht ook worden toegepast om aardbevingsvoorspelmodellen op hun betrouwbaarheid te testen, stellen Australische onderzoekers.

De wiskundige verklaring
Terwijl het aantal toepassingen toeneemt, is de vraag ‘hoe kan het dat de wet van Benford bestaat?’ nog steeds niet beantwoord.
Een wiskundige uitleg voor het patroon zonder in formules te vervallen is wel te geven.
Stel je een loterij voor waarbij loten worden verdeeld, met in volgorde oplopende nummers. Van tevoren weet je niet hoeveel mensen er mee gaan doen.
En stel je voor: de opkomst is laag en er doen maar negen deelnemers mee, die lotnummers één tot en met negen krijgen toegewezen. Op dat moment is de kans op elk lotnummer ongeveer elf procent.
Maar stel je nu voor dat negentien mensen zich inschrijven, die dus de lotnummers één tot en met negentien krijgen. Dan is de kans dat je lotnummer met een één begint ineens meer dan vijftig procent.
Loopt de loterij tot 99, dan is de kans dat je lot met een negen begint weer even groot als wanneer het met een één begint: elf procent. Maar loopt het aantal deelnemers verder op, tot bijvoorbeeld 250 deelnemers, dan is de kans het grootst dat het lotnummer begint met een één (namelijk: lotnummer 1, 10-19 en 100-199) en heb je met een lotnummer dat begint met een 2 (2, 20-29 en 200-250) ook nog een gerede kans.
Lotnummers die met een ander cijfer beginnen, komen vele malen minder vaak voor.

Als je de reeks lotnummers oneindig lang maakt, en dan naar de spreiding kijkt, vormen getallen die met het cijfer 1 beginnen 30,1 procent van het geheel. Getallen die beginnen met een twee vormen ongeveer 17 procent en getallen die beginnen met een negen zijn er minder dan vijf procent. Dat is de ideale Benfordverdeling (het rode lijntje in alle bovenstaande grafieken), die je ook kunt berekenen met een door Frank Benford opgestelde wiskundige formule.
Wie bovenstaande uitleg liever in beeld krijgt, kijkt naar deze aflevering van het onvolprezen YouTube-kanaal Numberphile (Engelstalig).
Tot zover de wiskundige uitleg achter de wet van Benford.
Maar die verklaart nog niet waarom de wet geldt voor heel veel menselijke en natuurlijke processen.

Het grote waarom
Een veelgehoorde verklaring is dat de wet een intrinsieke eigenschap is van ons rekenkundig systeem. Het resultaat van onze wiskundige kijk op de kosmos.
Zoals we de gulden snede terugzien in de natuur en in de wiskundige reeks van bovengenoemde Fibonaccigetallen, die op haar beurt weer voldoet aan de wet van Benford, zo zie je de wet van Benford terug in biologische, natuurkundige, sociologische en wiskundige fenomenen. Ook als we tot zestien op onze vingers zouden tellen in plaats van tot tien, zou de wet stand houden.
Op elke wiskundig gedefinieerde reeks cijfers blijkt er wel een uitzondering te vinden waarbij de wet in het geheel niet opgaat
Maar Theodore P. Hill, de wiskundige die wordt geroemd als degene die de meest volkomen wiskundige verklaring heeft gegeven voor het patroon, schreef vier jaar geleden dat hij het toch nog niet begrijpt.
Op elke wiskundig gedefinieerde reeks cijfers blijkt er wel een uitzondering te vinden waarbij de wet in het geheel niet opgaat. Daarnaast valt niet te definiëren wanneer je kleinere en grotere afwijkingen van de ideale Benfordgrafiek kunt verwachten.
‘Hoewel we voor veel facetten van de wet van Benford nu een degelijke verklaring hebben, is er op dit moment geen eenduidige benadering die het voorkomen ervan in dynamische systemen, getaltheorie, statistieken en data uit de echte wereld verklaart’, schrijft Hill. Hij noemt de wet ‘een mysterieus juweel’.
Daar moeten we het dus voorlopig mee doen.
Toch vervult de wet van Benford daarmee nog een nuttige functie. Wie naar het juweel kijkt, ziet hoe goed mensen zijn geworden in wiskunde en in het verzinnen van intrigerende toepassingen die weer tot nieuwe inzichten leiden.
En hoe moeizaam ze daarmee vervolgens de raadselen van het leven en het universum doorgronden.
Met dank aan Sebastian Kersten en Jules Stuifbergen.

