Met deze formule verander je van mening
Let op: laat kinderen onder de 9 niet meekijken!

Ooit geloofde ik in Sinterklaas.
Op een dag, lang na december, wandelde ik mijn vaders werkkamer binnen. En daar zag ik ze hangen: de tekeningen die ik had gemaakt voor de goedheiligman en een paar maanden daarvoor in mijn schoen had gestopt.
‘Hoe komen die daar?’ vroeg ik.
‘Oh ja’, antwoordde mijn vader met een nonchalance die ik nog altijd indrukwekkend vind, ‘die had Sinterklaas verloren toen hij door het huis liep.’
Ik was gerustgesteld.
Maar toen kwam er een Sinterklaas bij ons op bezoek die verdacht veel leek op buurman Jaap. En toen ik op zoek ging, vond ik ingepakte cadeaus verstopt op de kamer van mijn broer.
Het bewijs was te overweldigend: ik geloofde niet meer in Sinterklaas.
Update je overtuigingen
We hebben allemaal overtuigingen. En als het goed is, passen we die aan als er nieuwe relevante informatie beschikbaar komt. Zoals econoom John Maynard Keynes zou hebben gezegd: ‘When the facts change, I change my mind. What do you do, Sir?’
(Het citaat wordt vaak aan Keynes toegeschreven, maar de woorden zijn niet terug te leiden tot de econoom.)
Neem de feiten over corona. Helpen mondkapjes? Hoelang ben je immuun? Verspreidt het virus zich via aerosolen? Allemaal onderwerpen waar we langzaamaan meer van weten.
Net als ik met Sinterklaas, hadden wetenschappers waarschijnlijk een hypothese. Wel, niet, misschien... En naarmate er meer bewijs beschikbaar komt, passen ze hun blik aan. Belief updating, wordt dit ook wel genoemd.
Hoe je dat doet? Een predikant uit de achttiende eeuw heeft daar een antwoord op.
Wat is de kans dat Sinterklaas bestaat?
Thomas Bayes was een Engelse predikant en wiskundige. Na zijn overlijden publiceerde Richard Price zijn aantekeningen met daarin een parel, de stelling van Bayes.
Hier is-ie:
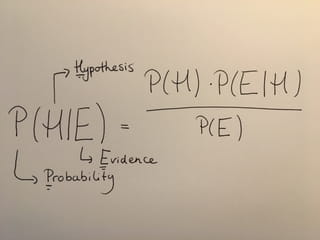
Je kunt er misschien niet meteen chocolade van maken, maar je ziet wel hoe eenvoudig de formule is. Eén regeltje maar. En vrij gemakkelijk te bewijzen, als je het een en ander weet van kansberekening.
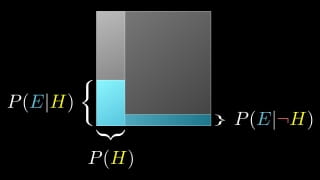
De H is je hypothese, in mijn geval dat Sinterklaas bestaat. Laten we zeggen dat ik vrij zeker was van mijn zaak en dat mijn P(H) – de kans dat hij echt is, dat de hypothese klopt – gelijk was aan 0,9 (90 procent).
Die kans wordt de ‘prior’ genoemd, want het is de kans die je iets toedicht voordat er nieuwe informatie beschikbaar komt.
Maar dan zie ik de tekeningen op de muur in mijn vaders werkkamer. Wat is nu de kans dat Sinterklaas bestaat? De stelling van Bayes helpt om die kans te berekenen. Je berekent de P(H|E), de kans dat de hypothese klopt gegeven (dat is het verticale streepje) dat je bepaalde ‘evidence’ hebt gezien.
Dit is de ‘posterior’, de kans die je je hypothese toedicht nadat je het nieuwe bewijs meer hebt genomen.
Om het helemaal te berekenen hebben we nog wat extra ingrediënten nodig. Namelijk: de P(E), de kans dat ik die tekeningen voor Sinterklaas aan de muur van mijn vader zie hangen. Ik ga er voor het gemak van uit dat mijn vader zo’n fan is van mijn werk dat hij gevonden tekeningen sowieso aan de muur hangt; die kans is dus 1.
Er zijn twee manieren dat ik de tekeningen kan observeren, namelijk:
- Sinterklaas bestaat én hij verliest mijn tekeningen (die dus gegarandeerd op mijn vaders muur belanden). Ik vond het vrij verbazingwekkend dat die tekeningen daar hingen, dus laten we zeggen dat – als Sinterklaas echt bestaan had – ik de kans dat hij mijn tekeningen zou verliezen op 0,2 had geschat. Deze situatie kun je wiskundig opschrijven als: P(H)*P(E|H)=0,9*0,2=0,18.
- Sinterklaas bestaat niet én ik zie de tekeningen, sowieso, op mijn vaders muur hangen. Dit kun je weer opschrijven als: P(¬H)*P(E|¬H)=0,1*1=0,1. (Die haak betekent 'niet', dus P(¬H) is de kans dat de hypothese niet klopt.)
Tellen we die twee kansen bij elkaar op, dan hebben we de kans dat ik de tekening aan de muur zag hangen: P(E)=0,18+0,1=0,28. Nu kun je de rest van de formule invullen:
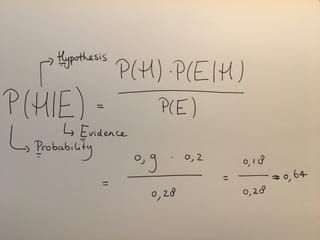
Mijn ‘posterior’ is dus gelijk aan (afgerond) 0,64. Had ik eerst een sterke overtuiging dat Sinterklaas bestaat (0,9), nu is dat minder. Maar nog steeds acht ik de kans groter dan 50-50 dat hij wel degelijk bestaat. Komt er nog een bewijsstuk, buurman Jaap bijvoorbeeld, dan zou dat zomaar kunnen omslaan.
In deze video van 3Blue1Brown duik je verder in de stelling van Bayes:
En wat dan nog?
Het is natuurlijk niet alsof ik als kind die berekeningen aan het maken was. Maar het idee achter het proces past wel bij hoe we denken. We hebben voorkennis, leren nieuwe dingen, en passen daarmee ons beeld van de werkelijkheid aan. Of je de wiskunde nu gebruikt of niet, de les is: gebruik nieuwe informatie, maar met mate.
Zoals epidemioloog Marc Lipsitch stelt: ‘Een van de uitersten is om te beslissen wat je denkt en ongevoelig te zijn voor nieuwe informatie. Een ander uiterste is om aan het laatste wat je geleerd hebt te veel waarde toe te kennen. In grote lijnen volgt het Bayesiaanse redeneren basale principes om wat je eerder dacht te integreren met wat je hebt geleerd en tot een conclusie te komen waarin beide zijn meegenomen, met het gepaste gewicht.’
Hij vertelt dit in een goed artikel in The New York Times, waarin meer wordt uitgelegd over hoe je Bayesiaans denken kunt toepassen in de coronacrisis.
Dat is overigens lang niet de enige toepassing. De formule wordt gebruikt in rechtszaken, in spamfilters, bij wetenschappelijk onderzoek. Zelfs bij schatzoeken heeft de Bayesiaanse benadering zich bewezen. En ken je Clippy nog, de irritante paperclip die je lastigviel in Windows? Ook die gebruikte Bayes.
Tot slot nog een goede tip van statisticus David Spiegelhalter. Hij verwijst in hetzelfde New York Times-artikel naar de Wet van Cromwell: geef iets nooit 100 procent of 0 procent kans. Met andere woorden, reserveer een beetje ruimte voor de twijfel.
‘Houd een beetje achter – met een klein beetje kans, een pietepeuterig beetje – voor het geval dat je ongelijk hebt’, adviseert Spiegelhalter. ‘Als er dan nieuw bewijs langskomt dat volledig in tegenspraak is met je eerdere overtuiging, dan kun je snel weggooien wat je eerder dacht en overstappen naar die nieuwe manier van denken.’
Daar is niets wiskundigs aan. ‘En het hoeft niet per se technisch of formeel te worden gedaan; het kan gewoon in je achterhoofd zitten als een idee. Noem het “nederigheid modelleren”. Je kunt het mis hebben.’
Dus wie weet bestaat Sinterklaas wel.
Tot slot...
...sprak ik met cabaretier Pepijn Schoneveld in zijn podcast PepTalk. Een fijn (en gezellig!) gesprek over onzekerheid. Een ode aan de twijfel.