Een van de misleidendste grafieken die ik ooit zag (en mijn optreden bij De Slimste Mens)
Op 14 december 2015 tweette de National Review - een conservatief Amerikaans tijdschrift - ‘de enige klimaatveranderinggrafiek die je hoeft te zien.’ Op het plaatje zag je de temperatuur sinds 1880.
Wat bleek? De gemiddelde temperatuur was de afgelopen 135 jaar nauwelijks veranderd. De oranje lijn was zo vlak als de hartmonitor van een overleden patiënt. Je kon de piep bijna horen.
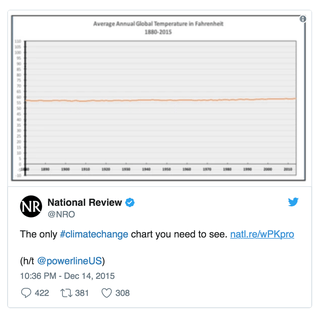
Mijn eerste reactie: die data moeten fout zijn. Hoe vaak had ik wel niet gehoord over stijgende temperaturen, hét argument om bewuster met het klimaat om te gaan?
Maar de data klopten. En kwamen van een betrouwbare bron: de NASA, de Amerikaanse ruimteorganisatie. En toch is deze grafiek een van de meest misleidende die ik ooit heb gezien.
Potemkingetallen
Op oudejaarsdag leverde ik bij de redacteur van mijn boek een hoofdstuk in over getallenfraude. Denk aan de ‘anderhalf miljoen’ publiek bij Donald Trumps inauguratie of de datasets van Diederik Stapel.
Schrijver en wiskundige Charles Seife noemt zulke nepcijfers ook wel ‘Potemkingetallen,’ naar de Russische gouverneur die nepdorpen zou hebben gebouwd om indruk te maken op Catharina de Grote.
Potemkins huizen zagen er geloofwaardig uit - er dartelde zelfs wat nepbevolking tussendoor - maar achter de gevels zat helemaal niets.
(Dit verhaal over Potemkin is misschien weer een Potemkinverhaal, aangezien historici het in twijfel trekken.)
Hoe stuitend dit soort cijfermanipulatie ook is, het lijkt maar een deel van het probleem. In de jaren dat ik over statistiekmisbruik schrijf, kwam ik vaak veel subtielere misleiding tegen.
Cijfers waar, anders dan bij de Potemkingetallen, wél iets achter zat.
Ik ben nooit ouder geworden
En zo komen we terug bij de grafiek in National Review, die gebaseerd is op betrouwbare data. Waarom is ze toch niet in de haak?
Het antwoord ligt in de verticale as: die loopt van -10 tot 110 Fahrenheit, omgerekend is dat -23 tot 43 graden Celsius.
Nu klinkt dat nog wel oké, want er zijn plekken ter wereld die zo koud (Siberië) of zo warm (Las Vegas) kunnen worden.
Maar het gaat hier om de gemiddelde temperatuur op de wereld. En daar kan een paar graden al een enorm verschil maken. Klimaatexperts zijn het erover eens dat een opwarming van 2 graden al catastrofale gevolgen heeft.
Met zijn y-as verbloemt de National Review zo veranderingen die ertoe doen. Het is alsof ik de grafiek hieronder bekijk en concludeer dat ik tijdens mijn leven niet ouder ben geworden.
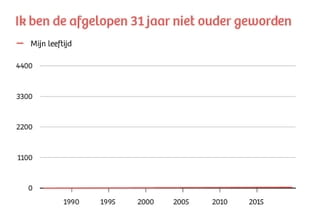
Pas je de as van de National Review-grafiek aan, dan krijg je ineens een heel ander beeld:
Het is dit soort subtiel statistiekmisbruik dat moeilijk te bestrijden is, want je ziet de misleiding pas als je de context kent. Je moet weten welke temperatuursverandering consequenties heeft. En dat de National Review een conservatief blad is dat bekendstaat om zijn klimaatscepsis.
Zoals dit Vox-filmpje stelt: ‘Y-assen liegen niet tegen mensen.’ Mensen liegen tegen mensen.
#NerdAlert
Op Tweede Kerstdag deed John Pace - een 51-jarige elektrotechnicus uit Tennessee - een bijzondere ontdekking: het grootste priemgetal ooit gevonden.
Priemgetallen kunnen alleen door één en door zichzelf gedeeld worden en zijn de obsessie van menig getallennerd. Bovendien zijn ze heel belangrijk als je veilig wilt internetten.
De nieuwe vondst telt 23 miljoen cijfers en is een ‘Mersenne-priemgetal.’ Zo’n getal krijg je als je een heleboel tweeën met elkaar vermenigvuldigt en daarna een één aftrekt (die som leidt niet altijd tot een priemgetal, dus je moet daarna checken of het resultaat inderdaad alleen door één en zichzelf gedeeld kan worden.)
In dit geval: twee tot de macht 77.232.917 min één.
(Liefhebbers kunnen het getal downloaden, maar print het niet uit: het beslaat bijna negenduizend kantjes.)
Pace deed mee aan het Great Internet Mersenne Prime Search (GIMPS)-project. Net als duizenden andere vrijwilligers liet hij software draaien die eindeloos tweetjes met elkaar vermenigvuldigde en de resultaten controleerde. Zijn computer moest zes dagen fulltime rekenen voordat de nieuwe priem was gevonden.
Goed nieuws: Euclides bewees in 300 voor Christus al dat er eindeloos veel priemgetallen bestaan. Op naar de volgende!
Tot slot...
...zat ik op 1 januari in het spelprogramma De Slimste Mens. Nog niet gezien? Je kunt de aflevering terugkijken op de website.
Met dank aan Leon de Korte.
Aanvulling 9 januari 10.30 uur: Met dank aan de opmerkingen in de bijdragensectie is het onderdeel over de priemgetallen nog iets aangescherpt.
Tot de volgende!
Sanne Blauw

