Dit is het belangrijkste getal van de pandemie. Hoe wordt het berekend?

Het is van een ‘allesoverstijgend belang dat [de] verspreidingsgraad onder de 1 ligt’, stelde Mark Rutte in de persconferentie op 28 april, waarin hij bekendmaakte dat de scholen en kinderopvang langzaamaan open zullen gaan.

Sinds een tijdje ligt die graad in Nederland inderdaad onder de 1. Stijgt hij boven die grens, zei Rutte ook, dan twijfelt hij niet om weer strengere maatregelen in te voeren.

Hierbij vaart hij op het advies van het Outbreak Management Team (OMT), dat vindt dat maatregelen pas versoepeld kunnen worden als de besmettingsgraad ‘geruime tijd’ kleiner is dan 1.

Een belangrijk getal, dus, die besmettingsgraad. Hoe wordt hij berekend?

Hoe zat het ook weer met die R?

De besmettingsgraad die Rutte noemde wordt ook wel het ‘besmettingsgetal’ of ‘reproductiegetal’ genoemd. Of, voor intimi: R.

Twee termen worden nog weleens door elkaar gehaald: R0 en R. R0 is het ‘basaal reproductiegetal’ – het gemiddeld aantal mensen dat een geïnfecteerd persoon besmet, in een populatie waar de ziekte voor het eerst komt en nog geen maatregelen zijn genomen. De R0 gaat er dus van uit dat iedereen nog besmet kan worden.

(Fun fact: de R0 is bedacht door de Nederlandse epidemioloog Hans Heesterbeek.)

R geeft een beeld van hoe de besmetting gaat

De R, daarentegen, is het ‘effectief reproductiegetal’ – het gemiddeld aantal mensen dat een geïnfecteerd persoon daadwerkelijk besmet. Die gaat dus niet meer uit van de hypothetische beginsituatie, maar geeft een beeld van hoe het in de praktijk gaat. Daarom is dat ook het getal waar je nu naar wilt kijken.

Deze R is doorgaans kleiner dan de R0, omdat er bijvoorbeeld maatregelen zijn genomen of er een vaccin gevonden is (helaas is dat nog niet het geval voor corona). Een ander verschil: R verandert door de tijd heen, R0 is een constante.

Hoe moet ik die R interpreteren?

Stel, R is op dit moment gelijk aan 2. Dat betekent dat één ziek persoon gemiddeld twee mensen besmet. Die besmetten op hun beurt elk twee mensen, dus in totaal vier. Het aantal nieuwe besmettingen verdubbelt dus per cyclus: 1, 2, 4, 8, 16, 32...

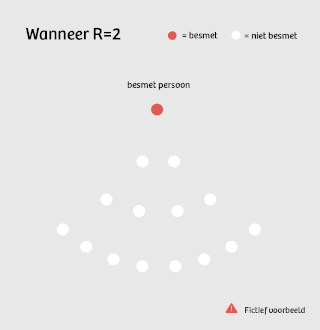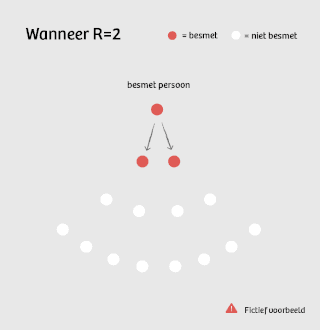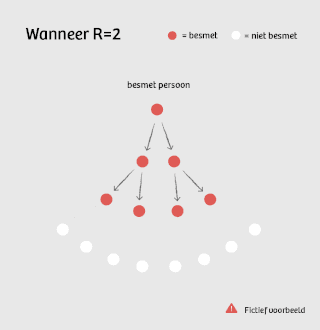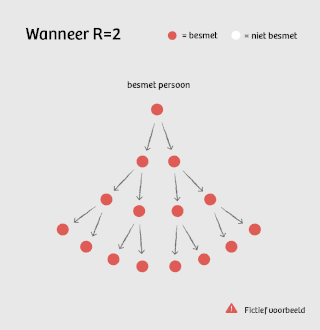
Dit is wat je noemt exponentiële groei – een ontwikkeling die niet lineair verloopt, maar steeds sneller toeneemt.

Is die R gelijk aan 1, dan is er geen toename meer van nieuwe patiënten, maar ook geen afname: 1, 1, 1, 1, 1, ... Dan is de ziekte ‘endemisch’, het aantal nieuwe besmettingen verloopt redelijk constant.

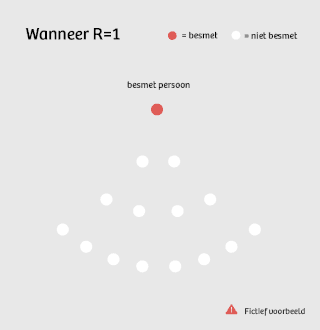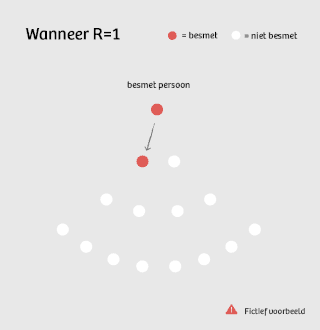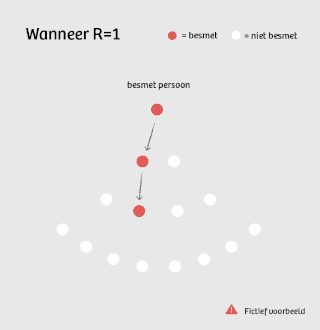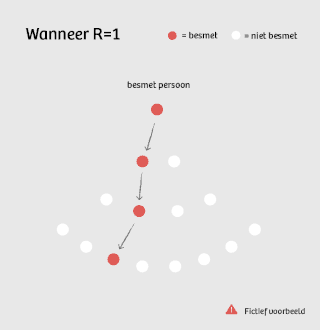
Waar het OMT dus op mikt, is een R onder de 1. Voor elk geïnfecteerd persoon komt dan gemiddeld genomen minder dan 1 persoon in de plaats.

Stel, de R is 0,8 en we hebben vandaag de dag 10.000 besmettelijke mensen rondlopen (dit is een fictief getal). Dan is dit het verloop van nieuwe patiënten: 10.000, 8.000, 6.400, 5.120, 4.096... De ziekte dooft dan dus steeds verder uit. Daarom is het zo belangrijk dat die R onder de 1 terechtkomt.

Een klein verschil in de R kan al enorm verschil maken, zo legt professor Merkel uit in dit filmpje.

Youtube plaatst cookies bij het bekijken van deze video Bekijk video op Youtube

Hoe hangt de R af van de maatregelen?

De R wordt beïnvloed door drie factoren:

• De kans dat iemand een ander besmet bij contact (p)
• De hoeveelheid contacten per tijdseenheid (c)
• De duur van besmettelijkheid (d)

Vermenigvuldig je die drie met elkaar, dan krijg je de R:

Het mooie van die formule is dat je precies ziet aan welke knoppen je kunt draaien als je de R wilt veranderen. Verklein je een van de onderdelen, dan verlaag je daarmee ook de R.

Neem de kans dat iemand een ander besmet (p). Die kans kun je verlagen door handen te wassen, door afstand te houden en – hopelijk straks – door mensen te vaccineren.

Het aantal contacten per tijdseenheid (c) kun je verlagen door thuis te gaan werken, door evenementen af te gelasten en horecagelegenheden te sluiten. Ook het sluiten van scholen volgde deze beredenering, al is het steeds waarschijnlijker dat kinderen weinig besmettelijk zijn.

Tot slot, kun je de duur van besmettelijkheid (d) bijvoorbeeld verkorten door ziektegevallen snel op te sporen en te isoleren. Daarom wil Hugo de Jonge ook zo graag een app, al is nog onduidelijk hoe effectief zo’n ding zal zijn (nog daargelaten of je het überhaupt moet willen).

Hoe berekent het RIVM de R?

Het reproductiegetal is gemakkelijk te berekenen als je weet wie wie geïnfecteerd heeft. Per patiënt zoek je uit hoeveel anderen diegene heeft besmet, je neemt het gemiddelde en – voilà – je hebt je R.

Maar dat is intussen onhaalbaar geworden. Er zijn simpelweg te veel coronagevallen om precies na te trekken wie er door wie besmet is geraakt. Daarom heb je een statistische methode nodig die op een andere manier dat reproductiegetal probeert te berekenen.

Het RIVM gebruikt niet die p*c*d-formule die we hierboven zagen, omdat die onderdelen lastig te berekenen zijn. Het baseert zijn model op een artikel van Jacco Wallinga, hoofd van de afdeling Modellering van Infectieziekten bij het RIVM, en Harvard-epidemioloog Marc Lipsitch.

Deel het aantal mensen dat ziek is op dit moment door het aantal dat een generatie-interval geleden ziek was – en je hebt de R

Een belangrijk ingrediënt voor het model is het ‘generatie-interval’: de periode tussen het moment dat iemand geïnfecteerd raakt en het moment dat diegene een ander infecteert. Het grove idee: deel het aantal mensen dat ziek is op dit moment door het aantal dat een generatie-interval geleden ziek was – en je hebt de R.

Welke data worden gebruikt?

Maar dan moet je wel betrouwbare cijfers hebben. En dat is lastig als het op corona aankomt. Het aantal (sterf)gevallen is namelijk een onderschatting, omdat er niet vrijuit getest wordt.

Daarom gebruikt het RIVM ziekenhuisdata, afkomstig van de Nationale Intensive Care Evaluatie (NICE). NICE houdt cijfers bij van opnames in het ziekenhuis en, specifieker, op de intensive care. In het systeem Osiris registreren ziekenhuizen wanneer iemand is opgenomen en wanneer de eerste dag was dat iemand ziek werd. Met die eerste ziektedag gaan de modelleurs bij het RIVM terugrekenen hoe hoog het reproductiegetal moet zijn geweest.

Die ziekenhuisdata zijn vrij hard, omdat er in ziekenhuizen veel getest wordt. Ook belangrijk: de maximale capaciteit in ziekenhuizen is gelukkig nooit behaald. Daarom is aan te nemen dat alle ernstige gevallen in deze data zijn opgedoken en dat deze cijfers een goede indicator geven van de proportie ernstig zieke patiënten in de bevolking.

Een belangrijke kanttekening: als bepaalde groepen niet naar het ziekenhuis komen – zoals nu soms voor ouderen het geval is – dan kunnen ze dit getal niet beïnvloeden. Dus die R zegt alleen iets over het deel van Nederland dat in het ziekenhuis terecht kan komen. Als er uitbraken in verpleeghuizen zijn, dan zal de werkelijke R hoger liggen.

Hoe betrouwbaar is de R?

Ook aan ziekenhuisdata zitten wat haken en ogen. Zo kun je niet altijd met zekerheid vaststellen wanneer iemand ziek is geworden.

Ook is de berekening van R per definitie vertraagd, omdat de eerste ziektedag van nieuwe patiënten – waarmee het RIVM rekent – al een aantal dagen terug in het verleden ligt als iemand in het ziekenhuis belandt.

Daarnaast is er vertraging in de registratie van gevallen, al helemaal in het weekend. Daarom komt het vaak voor dat ziekenhuisopnames pas een paar dagen later opduiken in de data.

Al met al zit er dus nog zeker wat onzekerheid in de modellen. Daarom zie je in de grafieken van het RIVM ook altijd een bandbreedte – dat is de onzekerheidsmarge. Zie bijvoorbeeld de grafiek die Jaap van Dissel op 22 april aan de Tweede Kamer liet zien.

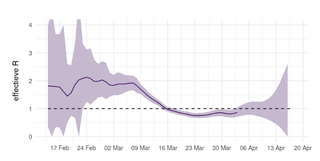
Intussen is deze grafiek alweer gedateerd, maar de conclusie is ook vandaag relevant: de R zou wat hoger, maar ook wat lager uit kunnen vallen. En voor de laatste periode is de onzekerheidsmarge zo groot dat je eigenlijk geen uitspraak kunt doen over de R.

Het is dus altijd achteraf gepraat, die R.

Dus als de R onder de 1 ligt, is alles in orde?

Op 1 maart 2003 kwam de 23-jarige Esther Sally Mok terecht in Tan Tock Seng Hospital in Singapore. Ze was een paar dagen geleden teruggekomen van een reisje naar Hong Kong en nu voelde ze zich niet lekker.

Mok zou de geschiedenis ingaan als de eerste SARS-patiënt in Singapore. Op 25 maart overleed haar vader. Een dag later haar pastoor. Ook haar moeder zou overlijden. In totaal heeft Mok ten minste 24 mensen besmet.

De R is slechts een gemiddelde. Als 35 mensen niemand besmetten en één 24, zoals bij het eerste SARS-geval, dan ligt de R onder de 1 (24 besmettingen gedeeld door 36 personen is gelijk aan 2/3).

Superverspreiders spelen een belangrijke rol bij het coronavirus

Toch zie je dat er uitbraken kunnen ontstaan, omdat zo’n ‘superverspreider’ ineens veel mensen kan besmetten. RIVM-modelleur Jacco Wallinga zei eerder tegen Het Parool dat superverspreiders een belangrijke rol spelen bij het coronavirus.

Van Dissel stelde dan ook op 8 april dat je een R onder de 1 moet nastreven, maar dat dat niet meteen wil zeggen dat je maatregelen dan ook kunt loslaten. Hij liet het plaatje van de SARS-besmetting in Singapore zien.

En nog iets: dat de R onder de 1 ligt, betekent niet dat er ineens geen nieuwe gevallen meer zijn. Zelfs met een R van 0,5 verschijnen bij 10.000 geïnfecteerden over een paar dagen alsnog 5.000 nieuwe patiënten.

Hoe gaat het nu in Nederland?

Lag de R in Nederland op het begin nog rond de 2, in maart zette het getal een duikvlucht in. Ergens half maart dook het onder de magische grens van 1.

Half maart? Wacht eens even, dat was toch toen de scholen en horecagelegenheden sloten? Was dat dan wel nodig?

Tsja, dat is lastig te zeggen, want we weten niet hoe de lijn was verlopen als er geen maatregelen waren genomen. Misschien was het wel boven de 1 blijven hangen. Hoogleraar infectieziektemodellering Sake de Vlas (Erasmus MC) zei in de Volkskrant: ‘Ik denk dat de stappen op 12 en 16 maart nodig waren om de curve verder naar beneden te duwen.’

Sowieso is er veel tegelijk veranderd, dus het is lastig om in te schatten wat ervoor heeft gezorgd dat die R omlaaggaat. Nu sommige maatregelen worden versoepeld, en andere niet, zal hopelijk blijken in hoeverre ze invloed hebben op de R.

En wil je de laatste stand van zaken weten? Kijk dan online naar de technische briefing voor de Tweede Kamer, waar Jaap van Dissel bijna wekelijks laat zien hoe het ervoor staat met de R in Nederland.

Verder lezen?