Na deze 4 grafieken kijk je nooit meer hetzelfde naar het gemiddelde

Wat hebben een donut en een dino met elkaar gemeen? Meer dan je denkt. En ze vertellen je een hoop over de zin en onzin van statistiek.
Gemiddelden zijn overal. Zo’n een op de twaalf Tweede Kamerstukken noemt het gemiddelde - van het gemiddelde brandstofverbruik van voertuigen* tot de gemiddelde wachttijd voor ggz-instellingen.*
Ook in de media regeert het gemiddelde. Zo berichtte de NOS afgelopen weekend over het gemiddeld bezoekersaantal van de website van het ministerie van Buitenlandse Zaken (‘210.000 keer per maand’),* de gemiddelde stijging van de WOZ-waarde (‘3,3 procent’)* en de gemiddelde leeftijd van de basis van het Chileense voetbalteam (‘boven de dertig’).*
Het gemiddelde reduceert een warrige hoop data tot een concreet getal. Handig, maar door die simplificering laat hij sowieso informatie achterwege. Daarom vangt hij niet alleen de werkelijkheid, maar vervangt haar ook.
Hoeveel zegt het cijfer dan nog? In die vraag bijt ik me al een tijdje vast. Vandaag alvast een stukje van de puzzel: waarom je verder moet kijken dan het gemiddelde.
Even rijk, even gelukkig, even overtuigd
Vaak gebruik je het gemiddelde om te vergelijken. Dat het gemiddelde inkomen van twintigers lager is dan tien jaar geleden, bijvoorbeeld.* Of dat Nederlanders gelukkiger zijn dan Belgen.*
Is het gemiddelde van twee groepen hetzelfde, dan zijn ze hetzelfde: even rijk, even gelukkig of even overtuigd dat html een seksueel overdraagbare aandoening is. Toch?Not so fast. Hetzelfde gemiddelde kan hele verschillende verhalen verhullen.
Eén gemiddelde, vier verhalen
Vier grafieken: een dinosaurus, een donut, een ster en een matrix. Wat hebben ze met elkaar gemeen, denk je?
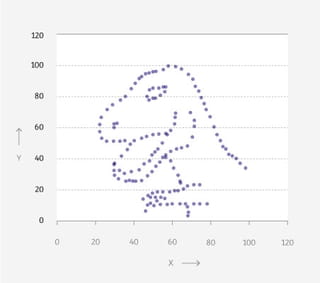
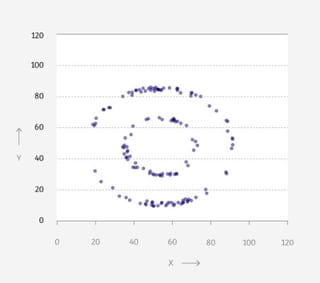
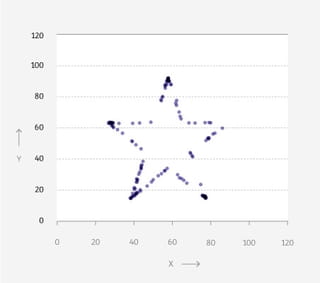
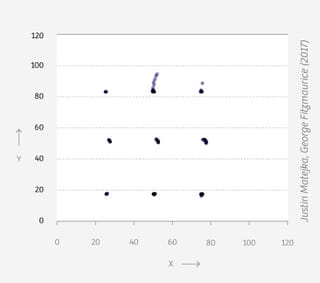
Op het eerste gezicht weinig. Je ziet telkens punten in een patroon, verder is er weinig wat de grafieken bindt.
Maar als je de achterliggende data bekijkt, lijken ze meer op elkaar dan je ziet. Want: de gemiddelden zijn voor alle vier hetzelfde. Tot wel twee cijfers achter de komma.
Elke grafiek vertelt een ander verhaal, maar in een gemiddeld nieuwsbericht waren ze niet te onderscheiden geweest.Nog twee klassiekers
Het wordt nog gekker. Want ook als we verder kijken dan het gemiddelde, lijken de grafieken griezelig veel op elkaar.
Neem een statistische evergreen: de standaarddeviatie. Die is handig als je geïnteresseerd bent in de spreiding. Als je bijvoorbeeld niet alleen het gemiddelde inkomen wil weten, maar ook hoe die inkomens verdeeld zijn.
Hoe zit dat hier? Liggen de punten in de ene grafiek verder uit elkaar dan in de andere?
Nope. Ook op de standaarddeviatie scoren de vier precies hetzelfde.
Nog een klassieker dan: de correlatie. Daarmee bereken je hoe sterk een verband is. Tussen geluk en inkomen, bijvoorbeeld. Of tussen bbp en CO2-uitstoot.
Is het verband in de ene grafiek sterker dan in de andere? Je ziet hem al aankomen: nee, ook de correlaties zijn gelijk.
Kortom, de grafieken zijn in veel statistische opzichten identiek. Alsof je een broodje kaas, een dame blanche, een zeewierburger en een Thaise curry eet, en ze smaken allemaal precieshetzelfde.
Meer voorbeelden
Het bovenstaande viertal is slechts één voorbeeld. In 1973 publiceerde Francis Anscombe vier grafieken die ook visueel verschillend maar statistisch identiek zijn.


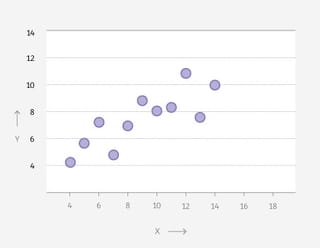
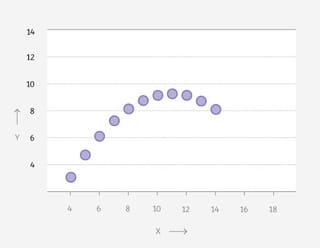
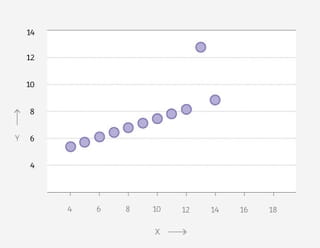
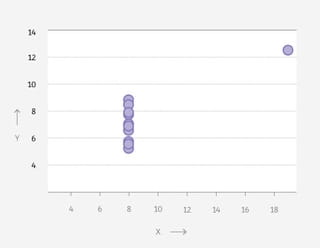
Geïnspireerd door ‘Anscombe’s kwartet’ bedachten onderzoekers Justin Matejka en George Fitzmaurice een methode om meer van dit soort grafieken te vinden.
Ze beginnen met een dataset en verleggen vervolgens de punten stukje bij beetje - zonder de statistische eigenschappen te veranderen - tot ze op hele andere data uitkomen. Op die manier kwamen ze van de ‘Datasaurus’ op de donut, de ster en de matrix.
Naast de vier grafieken van het begin, produceerden ze nog eens negen grafieken die óók dezelde statistische eigenschappen hadden. En met hun algoritme kun je nog veel meer variaties vinden.
Nogal wat voorbeelden dus, waar gemiddelden en andere statistiekjes je niet verder helpen. Moeten we dan maar kappen met die berekeningen? Nee, vond Anscombe. ‘Maak zowel berekeningen als grafieken,’ schreef hij in 1973. ‘Beide dragen bij aan het begrip.’
Met andere woorden: data kunnen niet zonder visualisatie. Maar ook niet zonder statistieken.
Dus?
De belangrijkste boodschap van Anscombe en consorten: een cijfer vertelt nooit het hele verhaal. Dezelfde getallen kunnen volslagen verschillende werelden verhullen. Werelden die je alleen ziet als je goed kijkt.
Dus lees je morgen iets over een gemiddelde in de krant? Kijk verder. Misschien vind je wel een dino.

